69.x的平方根

问题描述

分析加代码1

  第一种想法就是传统的二分算法，解题的依据是一个数的平方根一般不超过其1/2即√x<=x/2，但要注意特殊的情况1和0，这种情况单独讨论即可。这里注意mid的求法，如果不加一的话在最后会卡住，其他的没有什么问题了，就是正常的二分，代码如下：

class Solution {
    public int mySqrt(int x) {
        if(x==0)
        return 0;
        if(x==1)
        return 1;
        int left,right,mid;
        left=1;
        right=x/2;
        
        while(right>left){
            mid=left+(right-left+1)/2;
            if(mid>x/mid)
                right=mid-1;
            else 
                left=mid;
        }
        return left;
    }
}

上面的if判断中使用的是除法而不是乘法，是为了防止大整数溢出，除法可以有效避免这种情况。

分析加代码2

  这是大佬提供的题解，使用牛顿迭代法，不得不说虽然没有学过数分，但是好歹学过一点高数，这一刻被捻的稀碎啊，后面的就是借鉴大佬的分析思路。
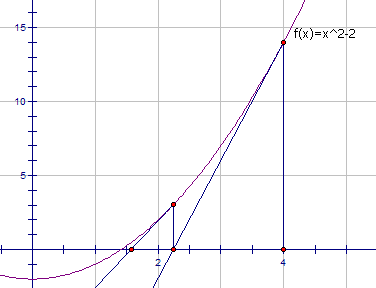
  下面这种方法可以很有效地求出根号a的近似值：首先随便猜一个近似值x，然后不断令x等于x和a/x的平均数，迭代个六七次后x的值就已经相当精确了。例子如下：
例如，我想求根号2等于多少。假如我猜测的结果为4，虽然错的离谱，但你可以看到使用牛顿迭代法后这个值很快就趋近于根号2了：

( 4 + 2/ 4 ) / 2 = 2.25
( 2.25 + 2/ 2.25 ) / 2 = 1.56944..
( 1.56944..+ 2/1.56944..) / 2 = 1.42189..
( 1.42189..+ 2/1.42189..) / 2 = 1.41423..

代码如下：

class Solution {
    int s;
    
 public int mySqrt(int x) {
     s=x;
     if(x==0) return 0;
    return ((int)(sqrts(x)));
  }
    
    public double sqrts(double x){
      double res = (x + s / x) / 2;
    if (res == x) {
      return x;
    } else {
      return sqrts(res);
    }
    } 
}

补充牛顿迭代法（我记得张宇讲过这个也是不断逼近的）

• 切线方程：以P为切点的切线方程：y-f(a)=f’(a)(x-a)
• 牛顿迭代：